Heinz Spiess
EMME/2 Support Center, Haldenstrasse 16,
CH-2558 Aegerten, Switzerlandheinz@spiess.ch
May 1990
In the past, many different models using observed link volumes to estimate or adjust O-D matrices have been proposed. While these models differ greatly in their mathematical formulation and interpretation, they all share the fact that using them for real size networks is difficult, if not impossible. This is due to the complexity of the computations that are involved and the need for very specialized software to carry them out. In this paper, we present a new gradient based model, which can and has been applied to large scale networks. Mathematically, the model is formulated as a convex minimization problem where, by following the direction of the steepest descent, we ensure that the original O-D matrix is not changed more than necessary. We show how this demand adjustment model can be implemented without the need to develop any new software, but only by using existing features of a standard transportation planning package (EMME/2). Since one iteration of the adjustment procedure consists essentially in two equilibrium assignments on the considered network, the method can be applied even to large scale networks and matrices. So far, our model has been applied successfully in several urban and national scale projects in Switzerland, Sweden and Finland, using networks with up to 522 traffic zones and 12460 links. Some results of these studies will be shown.
In almost all transportation planning applications, the input data which is the most difficult and expensive to obtain is the origin-destination demand matrix. Since the demand data cannot be observed directly, it must be collected by carrying out elaborate and expensive surveys, involving home- or road-based interviews or complicated number plate tagging schemes. By contrast, observed link volumes can be obtained easily and with reasonable precision by simply counting the traffic at certain countpost links, either manually or automatically, using mechanical or inductive counting devices.
Thus, it is not surprising that a considerable amount of research has been carried out to investigate the possibility of estimating or improving an origin-destination demand matrix with observed volumes on the links of the considered network.
Many models have been proposed in the past, see e.g . Van Zuylen and Willumsen (1980), Van Vliet and Willumsen (1981), Nguyen (1982), Van Zuylen and Branston (1982) and Spiess (1987). These models, while being very interesting from a theoretical point of view, have been of relatively little practical relevance so far. This is due to immense computation time and storage requirements that arise in practical implementations and which limit these approaches to very small problem sizes only. As to our best knowledge, none of these methods has so far been successfully applied to large scale networks with hundreds of traffic zones and thousands of network links.
Most of these "traditional" approaches can be formulated as convex
optimization problems in which the objective function corresponds to
some distance function ![]() between a "a-priori" demand matrix
between a "a-priori" demand matrix
![]() and the resulting demand g.
The constraints are then used to force the assigned volumes
and the resulting demand g.
The constraints are then used to force the assigned volumes ![]() to correspond
to the observed volumes
to correspond
to the observed volumes ![]() on the count post links
on the count post links ![]() .
(Note that in some formulations, such as Van Zuylen and Branston (1982),
these constraints are relaxed and, thus,
appear as additional terms in the objective functions.)
.
(Note that in some formulations, such as Van Zuylen and Branston (1982),
these constraints are relaxed and, thus,
appear as additional terms in the objective functions.)
In the following sections, we describe a new model which is suitable for large scale applications. We show how this model can be implemented without the need to develop any new programs, but by using the standard version of the transportation planning package EMME/2. Finally, we summarize the results of some urban and national scale applications in which the new model has been used recently.
In this paper a new type of model is proposed. It is also formulated as an optimization problem, but here the objective function to be minimized is a measure of distance between observed and assigned volumes. The simplest function of this type is the square sum of the differences, which leads to the following convex minimization problem:
subject to
![]()
where the ``pseudo''-function assign(g) is used to indicate the volumes resulting from an assignment of the demand matrix g. Of course, the particular assignment model used must correspond to a convex optimization problem, in order for (1) to be convex.
For the purpose of this paper, we shall assume that the term
assignment refers to an equilibrium assignment, where a set
of non-decreasing link cost functions ![]() on all links of the
network
on all links of the
network ![]() ensures the convexity of the model.
This type of equilibrium assignment problem has been extensively studied
and can be solved efficiently, either by the successive
linear approximation (Franck and Wolfe, 1956; Le Blanc et al., 1975; Florian,
1977) or the more recent PARTAN method (Florian et al, 1987;
Arezki and Van Vliet, 1990).
ensures the convexity of the model.
This type of equilibrium assignment problem has been extensively studied
and can be solved efficiently, either by the successive
linear approximation (Franck and Wolfe, 1956; Le Blanc et al., 1975; Florian,
1977) or the more recent PARTAN method (Florian et al, 1987;
Arezki and Van Vliet, 1990).
Since the matrix estimation problem as formulated in (1) is highly underdetermined, it usually admits an infinite number of optimal solutions, i.e. possible demand matrices which all reflect the observed volumes equally well. Of course, in the actual planning context, we expect the resulting matrix to resemble as closely as possible the initial matrix, since it contains important structural information on the origin-destination movements. Therefore, just finding one solution to problem (1) is clearly not enough.
``Traditional'' models eliminate (at least partially) this problem
of degeneracy by using an objective function Z(g)
which corresponds to a measure of distance ![]() and imposing
the equality between observed and assigned values as constraints.
While this approach indeed provides a mean to choose the ``best''
demand matrix (according to some criterion) among those satisfying
the conditions on the observed volumes, it also increases significantly the
complexity of the problem to be solved and, thus, contributes heavily to the
fact that these models are so difficult to apply to large scale problems.
and imposing
the equality between observed and assigned values as constraints.
While this approach indeed provides a mean to choose the ``best''
demand matrix (according to some criterion) among those satisfying
the conditions on the observed volumes, it also increases significantly the
complexity of the problem to be solved and, thus, contributes heavily to the
fact that these models are so difficult to apply to large scale problems.
If we would have a solution algorithm which inherently finds a solution
close to the starting point, we could leave the objective function
(1) as is.
Fortunately, the
gradient method![]() , also called the method of steepest descent,
has exactly this property that we look for. It follows always the
direction of the largest yield with respect to minimizing the objective
function and, thus, it also assures us not to deviate from the
starting solution more than necessary.
, also called the method of steepest descent,
has exactly this property that we look for. It follows always the
direction of the largest yield with respect to minimizing the objective
function and, thus, it also assures us not to deviate from the
starting solution more than necessary.
In the simplest case, when taking the gradient directly with respect to the variables g, the gradient method could be formulated as follows
where the ![]() have to be chosen small enough to ensure that the path
followed by the
have to be chosen small enough to ensure that the path
followed by the ![]() is sufficiently near to the true gradient path.
Note that we use the index i to denote an origin-destination pair (O-D pair),
and that the set of all active O-D pairs is I.
is sufficiently near to the true gradient path.
Note that we use the index i to denote an origin-destination pair (O-D pair),
and that the set of all active O-D pairs is I.
However, if the gradient is based on the variables g as in (3),
this implies that changes to the demand matrix are measured in an absolute
way, i.e. number of trips, regardless of the relative change this would
mean to the initial matrix. In particular, this would imply that
O-D pairs with ![]() would be affected by the adjustment as well.
would be affected by the adjustment as well.
For a more realistic approach the gradient should be based on the relative change of the demand, which can be written as
Note that when the relative gradient is used, the algorithm becomes multiplicative in ghi. Therefore, a change in demand is proportional to the demand in the initial matrix and, in particular, zeros will be preserved by the process.
Before turning our attention to the evaluation of the gradient ![]() , let us
first look at the decomposition of the link volumes
, let us
first look at the decomposition of the link volumes ![]() into path flows.
Let
into path flows.
Let ![]() denote the set of paths used for each O-D pair i, ieI, and
denote the set of paths used for each O-D pair i, ieI, and
![]() the vector of the corresponding path flows. The link volumes can then
be expressed as
the vector of the corresponding path flows. The link volumes can then
be expressed as
where

Using the path probabilities instead of the path flows
![]()
equation (5) can be rewritten as
We can now proceed to compute the gradient ![]() . Taking the derivative
of (1), we obtain
. Taking the derivative
of (1), we obtain
Assuming that the path probabilities are locally constant, we obtain from (8)
which, when inserted into (9), yields
In order to implement the gradient method 4, we also need to provide
values for the step lengths ![]() . Choosing very small values for the
step length has the advantage of following more precisely the gradient path,
but has the disadvantage of requiring more steps. On the other hand,
when choosing too large values for the step length, the
objective function Z(g) can actually increase and the convergence of
the algorithm would be lost. Thus, the optimal step length
. Choosing very small values for the
step length has the advantage of following more precisely the gradient path,
but has the disadvantage of requiring more steps. On the other hand,
when choosing too large values for the step length, the
objective function Z(g) can actually increase and the convergence of
the algorithm would be lost. Thus, the optimal step length ![]() at a given demand g can be found by solving the one-dimensional
subproblem
at a given demand g can be found by solving the one-dimensional
subproblem
subject to
Since the objective function Z is expressed in terms of the link volumes
![]() , we need to know how these change along the gradient direction.
This can be obtained by applying the chain rule to (10)
, we need to know how these change along the gradient direction.
This can be obtained by applying the chain rule to (10)
Solving the minimization problem (12) can be done by finding the zero of the derivative. Applying again the chain rule we obtain the derivative as
![]()
This leads directly to the optimal step length
which, in order to be feasible, needs only to be checked against and eventually be bounded by (13).
With the equations (11), (14) and (16), we have all the necessary results in order to solve the matrix adjustment problem (1) using the relative gradient method (4).
One major practical difficulty for applying matrix estimation models in practice is due to the fact that most models can only be implemented in highly specialized computer programs which are difficult to obtain and operate, if they exist at all.
In this section we show that the gradient method can be implemented using the standard version of the widely used EMME/2 transportation planning software (Spiess 1984; INRO 1989). Since Release 3.0 of EMME/2 (released October 1987), a feature of the car equilibrium assignment module known as Additional Options Assignment is available. The aim of this feature is to provide a general framework for the simultaneous computation of various path dependent informations which might be needed in addition to the usual assignment results.
Let us briefly look at the mathematical interpretation of this feature of EMME/2. (The emphasized terms in the paragraphs below correspond to the nomenclature used in EMME/2.)
For each path generated during the normal equilibrium assignment, an
additional path attribute ![]() is computed by combining the
additional link attributes
is computed by combining the
additional link attributes ![]() of the link on the path with the
path operator
of the link on the path with the
path operator ![]() (which can be any operator such as
(which can be any operator such as ![]() ,
,
![]() ,
, ![]() or
or ![]() )
)
![]()
Checking the path attribute ![]() against the specified path threshold
interval
against the specified path threshold
interval ![]() determines if the path is
included in the subsequent slave assignment of the additional
demand
determines if the path is
included in the subsequent slave assignment of the additional
demand ![]() . This way, the set of
active paths
. This way, the set of
active paths ![]() is defined.
is defined.
The results of the additional options assignment are the additional volumes
and the additional attribute matrix, which can be one of the following
Once we have expressed the additional options feature of EMME/2 in mathematical terms, it is evident that the framework does not only serve for the ``usual'' applications, such as link select analysis, partial assignments, or the computation of cost or distance matrices. It can also be used, as is, to implement the gradient method for the matrix adjustment problem, as described in the preceding section. The following paragraphs give an outline how this is achieved.
At the beginning of each iteration ![]() of the
gradient method, a ``plain'' equilibrium assignment (i.e. not using
the additional options feature) is carried out with the current demand,
in order to compute the link volumes
of the
gradient method, a ``plain'' equilibrium assignment (i.e. not using
the additional options feature) is carried out with the current demand,
in order to compute the link volumes
![]() i,
i, ![]() . With these volumes, the additional link attribute
. With these volumes, the additional link attribute
![]() is computed using the network calculator as
is computed using the network calculator as
![]()
The gradient matrix ![]() defined in (11) is next computed with
(22) as additional attribute matrix. This matrix is then used as
additional demand matrix
defined in (11) is next computed with
(22) as additional attribute matrix. This matrix is then used as
additional demand matrix ![]() and the variables
and the variables ![]() of (14)
are computed according to (18). The optimal step length
(16) is evaluated again with the network calculator.
Finally, the demand matrix is updated using the matrix calculator according
to (4).
of (14)
are computed according to (18). The optimal step length
(16) is evaluated again with the network calculator.
Finally, the demand matrix is updated using the matrix calculator according
to (4).
Using the macro feature of EMME/2, which allows the different modules of EMME/2 to be combined into more complex procedures, the entire algorithm can be packaged into one macro command, hiding all the implementational details from the user.
In terms of computation times, each iteration of the gradient method corresponds to one equilibrium assignment without additional options and two equilibrium assignments with additional options, plus some minor matrix and network calculations. While this is a substantial effort for every iteration, it is still doable even for the largest networks that can be handled in EMME/2, i.e. networks of up to 1600 traffic zones (2,560,000 O-D pairs!) and 32000 links.
During 1988 and 1989, we had the opportunity to test the proposed
gradient method and apply it in practice in several studies. The test example
used was based on the standard EMME/2 Winnipeg Demonstration Database. The
applications include two urban applications for the cities of Bern and Basel
and the two national road networks of Sweden and Finland![]() . The table below
gives some characteristics for the applications: number of traffic zones,
number of network links, number of links with observed volumes, the
. The table below
gives some characteristics for the applications: number of traffic zones,
number of network links, number of links with observed volumes, the
![]() -value between observed and assigned volumes using the initial
demand, the
-value between observed and assigned volumes using the initial
demand, the ![]() -value after the adjustment, and, finally, the number
of gradient iterations that were carried out for the adjustment.
-value after the adjustment, and, finally, the number
of gradient iterations that were carried out for the adjustment.
| Study | Zones | Links | Counts | initial | final | Iter. |
| Winnipeg | 154 | 2983 | 70 | 0.834 | 0.971 | 11 |
| Basel | 330 | 220 | 229 | 0.923 | 0.970 | 6 |
| Bern | 226 | 2676 | 338 | 0.960 | 0.995 | 20 |
| Sweden | 522 | 3879 | 334 | 0.827 | 0.992 | 20 |
| Finland | 469 | 12476 | 5759 | 0.491 | 0.886 | 30 |
As an example, the scattergrams of observed versus assigned volumes
before and after the adjustment are shown in Figures 1 and
2 below for the Swedish national road network application.
In Figure 3, the value of the objective function ![]() is shown for all 20 iterations. The computations were carried out on a SUN
SPARCstation 1 computer. On this equipment, each iteration of the gradient
method took about 25 minutes of computing time.
is shown for all 20 iterations. The computations were carried out on a SUN
SPARCstation 1 computer. On this equipment, each iteration of the gradient
method took about 25 minutes of computing time.
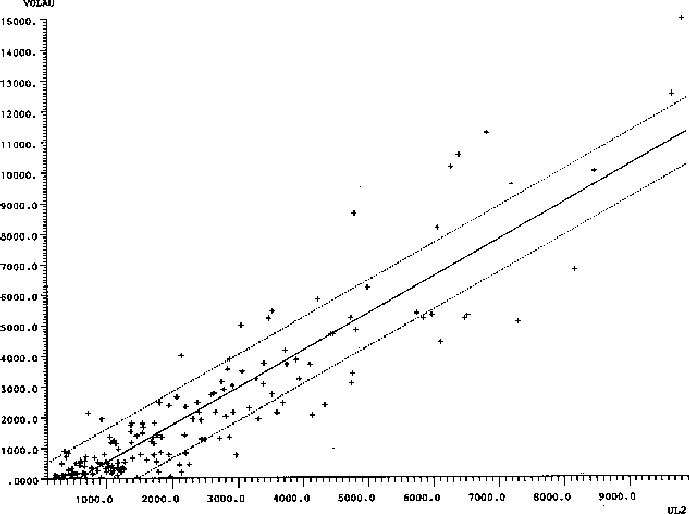
Figure 1: Assigned vs observed volumes before adjustment.
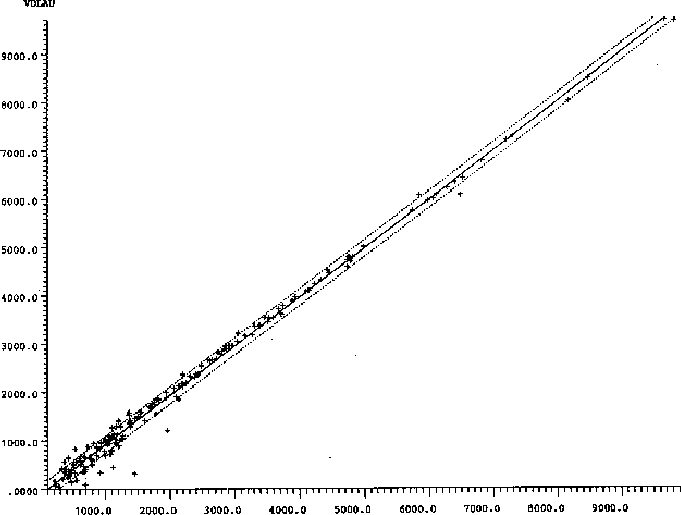
Figure 2: Assigned vs observed volumes after adjustment.
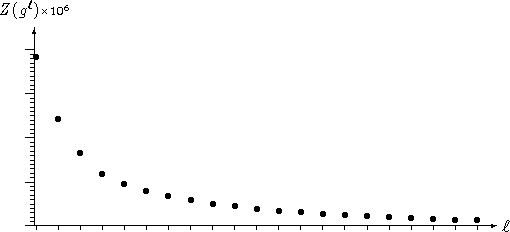
Figure 3: Values of the objective function ![]() .
.
In all applications that were carried out so far, the gradient method was found to perform very well. However, there are some important practical points to consider before applying the algorithm:
We have formulated a new type of matrix adjustment model in which the steepest descent property of the gradient method is used to overcome the degeneracy problem. Since this method will inherently find a solution which is close to the starting point, it is not necessary to address explicitly the degeneracy of the solutions in the objective function. The simplicity of the proposed method makes it applicable even to large scale problems.
In this model, the path probabilities ![]() need not to be stored
explicitly, since the gradient matrix
need not to be stored
explicitly, since the gradient matrix ![]() can be built up directly
as a by-product of the assignment. Therefore, the gradient model
is not restricted to proportional assignments models, but is
equally well applicable with the equilibrium assignment.
can be built up directly
as a by-product of the assignment. Therefore, the gradient model
is not restricted to proportional assignments models, but is
equally well applicable with the equilibrium assignment.
The method can be implemented without the need of any specialized software, but by just using the standard version of the EMME/2 transportation planning system. Therefore the gradient approach presented here is as much of theoretical interest as of practical importance, since it offers a simple analytic alternative to the still widely used practice of ``manual demand matrix calibration''.
Even though all applications so far were using equilibrium assignments on highway networks, the gradient approach which we have developed here is general enough to be applied to different assignment models. In particular, it could also be used in the context of transit networks. In this case, instead of the highway network equilibrium assignment, the transit assignment based on optimal strategies (see Spiess, 1984; Spiess and Florian, 1989) would be used. The mathematical formulation for the transit case, as well as some tests with real applications will be the topic of further research.
Finally, it is important to note that the objective function (1) used in this paper is only the simplest of many possible choices. The same gradient approach can equally well be used to solve problems with any other objective function of the form
Models of this type have been proposed by Willumsen (1984) and Brenninger-Göthe et al. (1989). The application of the gradient method in this more general context will be the topic of a forthcoming paper.