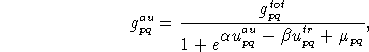
Even though the variable demand auto assignment has been available since the introduction of Release 4 in May 1989, it is still not as widely applied in practice as one might expect. One reason for this might be that we normally associate the variable demand assignment with full fledged multi-modal demand models in which complex demand or modal choice functions are estimated from survey results and socio-economic zonal data. Such models are, of course, not available for all applications. However, variable demand assignments can also be very useful in applications for which no such full demand or mode choice model has been calibrated. In this article, we show how to use the variable demand assignment to implement an incremental (or pivot point) mode choice model without any need for socio-economic data, by simply using the observed base year demand and impedances.
Consider the following standard bimodal logit mode choice demand function
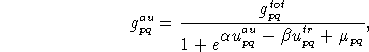
in which the auto demand ![]() is expressed as a function of the
total demand
is expressed as a function of the
total demand ![]() , the auto and transit impedances
, the auto and transit impedances ![]() and
and ![]() ,
and the combined effect of the socio-economic variables
,
and the combined effect of the socio-economic variables
![]() . Besides estimating the coefficients
. Besides estimating the coefficients
![]() and
and ![]() , the main effort in estimating a full demand model
is spent selecting the significant socio-economic variables
, the main effort in estimating a full demand model
is spent selecting the significant socio-economic variables ![]() and
estimating their coefficients
and
estimating their coefficients ![]() .
.
Assume now that we know for the base year the (observed) demand ![]() and
and ![]() , as well as the corresponding network impedances
, as well as the corresponding network impedances ![]() and
and
![]() . This information can be used to estimate the unknown
bias
. This information can be used to estimate the unknown
bias ![]() , by inserting the base year values into the above equation and
solving for
, by inserting the base year values into the above equation and
solving for ![]() , which yields
, which yields
![]()
These estimators can now be used to replace the combined effect of the socio-economic variables in the logit model. Doing so results in the following incremental mode choice function
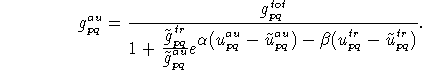
If we assume that the total demand is constant, the formula can further be simplified to obtain

Since the above demand function uses for each O-D pair the base year data as pivot point, this model will, if applied to the base year network, reproduce exactly the base year data (a property which does not hold for full demand models). If any change in the network is applied, the model computes the change in the auto demand due to the induced mode shift.
The incremental model only needs the specification of the two sensitivity
parameters ![]() and
and ![]() - a much easier task compared to the
calibration of a full mode choice function.
(Note that
- a much easier task compared to the
calibration of a full mode choice function.
(Note that ![]() is actually only needed if the
considered scenario includes changes in the transit impedances.)
Even if these coefficients are not known for a given application, it is
possible to use values from model calibrated for similar areas or to
test several values in the spirit of ``what if?'' games.
is actually only needed if the
considered scenario includes changes in the transit impedances.)
Even if these coefficients are not known for a given application, it is
possible to use values from model calibrated for similar areas or to
test several values in the spirit of ``what if?'' games.
If any socio-economic variable ![]() is also subject to change for the scenario
to be studied (such as changes in the parking costs), this can easily be
incorporated into the incremental model, by simply adding the term
is also subject to change for the scenario
to be studied (such as changes in the parking costs), this can easily be
incorporated into the incremental model, by simply adding the term
![]() to the argument of the exponential term.
to the argument of the exponential term.
For implementing this type of incremental logit function in a variable demand assignment, we need to define the corresponding EMME/2 auto demand function. In the simplest case, i.e. when considering changes in the auto network only and assuming fixed transit impedances, the following function can be used:
fa1 = (mat1+mat2)/(mat1+mat2*exp( ![]() *(upqau-mat3)))*mat1
*(upqau-mat3)))*mat1
where mat1= ![]() , mat2=
, mat2= ![]() and mat3=
and mat3= ![]() .
Note that the multiplication with mat1 was coded at the end of the
expression in order to avoid problems due to division by zero that otherwise
occur for O-D pairs with zero total demand.
The value sensitivity parameter
.
Note that the multiplication with mat1 was coded at the end of the
expression in order to avoid problems due to division by zero that otherwise
occur for O-D pairs with zero total demand.
The value sensitivity parameter ![]() can either be coded directly into
the demand function, or it can be stored in a scalar (where it can be modified
without recoding the function) and accessed in the
function via the ms() intrinsic.
can either be coded directly into
the demand function, or it can be stored in a scalar (where it can be modified
without recoding the function) and accessed in the
function via the ms() intrinsic.
If the scenario to be analyzed affects auto and transit impedances, the following function can be used:
fa2 = (mat1+mat2)/(mat1+mat2*exp( ![]() *upqau+mat3))*mat1
*upqau+mat3))*mat1
where mat1= ![]() , mat2=
, mat2= ![]() and
mat3=
and
mat3= ![]() (which is computed prior to the assignment with
module 3.21). Of course it would also be possible to use mat3, mat4
and mat5 to represent explicitly
(which is computed prior to the assignment with
module 3.21). Of course it would also be possible to use mat3, mat4
and mat5 to represent explicitly ![]() ,
, ![]() and
and ![]() ,
but computationally this would be much less efficient.
As can be seen from the above, incremental mode choice models can be
implemented very easily if the base year data is available for an
application, and -if carefully applied- provide important insight into
expected mode shifts that are likely to result from the studied network
interventions.
,
but computationally this would be much less efficient.
As can be seen from the above, incremental mode choice models can be
implemented very easily if the base year data is available for an
application, and -if carefully applied- provide important insight into
expected mode shifts that are likely to result from the studied network
interventions.