Generating Normally Distributed Random Numbers

In an earlier EMME/2 NEWS (No. 9, April 1990) we showed how the EMME/2 intrinsics put() and get() can be used to generate sequences of pseudo random numbers, using the linear congruential method. Assuming that not everyone has access to this issue, it is worthwhile to repeat the three EMME/2 expressions which yield uniformly distributed pseudo random numbers between 0 and 1 (each with a different cycle length):

  put(int(get(1)*430+2531).mod.11979)/11979

  put(int(get(1)*936+1399).mod.6655)/6655

  put(int(get(1)*1366+1283).mod.6075)/6075

As seen from the above expressions, the generation of uniform pseudo random numbers is quite simple. However, in many practical situations the need is not for uniformly, but for normally distributed random numbers. Thus, how can we generate random numbers that follow a normal distribution?

The standard way for generating deviates with a given distribution from uniform random numbers is to apply the inverse of the distribution function to the uniform values. Unfortunately, EMME/2 offers only a built-in intrinsic for the normal distribution function (erf()), but not for its inverse. Therefore, this method cannot be applied within EMME/2 expressions. Fortunately, it can be shown (see e.g. Handbook of Mathematical Functions by Abramowitz and Stegun) that if and are two independent uniform random variables, then is a normally distributed random variable with mean 0 and variance 1.

Using this relation, the expressions for linear congruent method given above can be transformed to new expressions that yield N(0,1) normally distributed pseudo random numbers as follows:

  sqrt(-2*ln((int(get(1)*430+2531).mod.11979+.5)/11979))*cos(6.28318531*(
  put(int((int(get(1)*430+2531).mod.11979)*430+2531).mod.11979)+.5)/11979)

  sqrt(-2*ln((int(get(1)*936+1399).mod.6655+.5)/6655))*cos(6.28318531*(
  put(int((int(get(1)*936+1399).mod.6655)*936+1399).mod.6655)+.5)/6655)

  sqrt(-2*ln((int(get(1)*1366+1283).mod.6075+.5)/6075))*cos(6.28318531*(
  put(int((int(get(1)*1366+1283).mod.6075)*1366+1283).mod.6075)+.5)/6075)

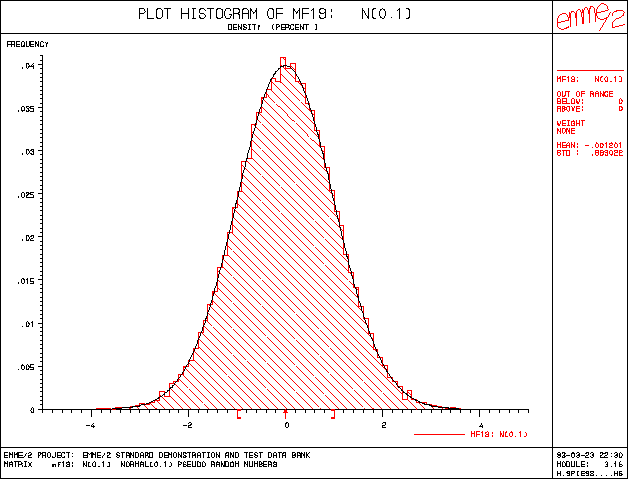
In the example below, a matrix has been computed with module 3.21 using the first of the above expressions. The density histogram of the matrix, produced with module 3.16, shows the typical ``bell'' shape of the normal distribution.