![]() First draft! -- Subject to revision!
First draft! -- Subject to revision! ![]()
Please let me know of any errors and typos you find - thanks!
Heinz Spiess
EMME/2 Support Center, Haldenstrasse 16, CH-2558 Aegerten, Switzerland
November 1996
The purpose of the note is to look at the problem of biproportional matrix balancing when the upper bounds are imposed on the matrix elements. This problem can be formulated as a convex minimization problem. Using the Kuhn-Tucker optimality conditions the functional form of the resulting model is derived. The dual formulation of the problem is derived and it is shown how it can be solved by a cyclic coordinate descent method. This leads to the proposal of an efficient solution algorithm.
![]() First draft! -- Subject to revision!
First draft! -- Subject to revision! ![]()
Please let me know of any errors and typos you find - thanks!
A PDF version of this document is also available.
The purpose of this note is to analyze an extension of the standard biproportional matrix balancing (Murchland 1977), also referred to as ``Fratar'' (Lamond and Steward 1981), ``Furness method'' (Furness 1970), ``maximum entropy transportation model'' or ``maximum entropy spacial interaction model'' (Florian ...?), and referred to as ``two-dimensional matrix balancing'' in the EMME/2 transportation planning package (Spiess 1984, INRO 1996).
As in the standard two-dimensional balancing, a given matrix (containing synthetic friction factors or ``prior'' matrix data) is ``factored up'' to a fit a given set of productions and attractions. But in addition to satisfying the given productions and attractions, upper bounds are now imposed on the elements of the resulting matrix. Such bounds can be thought to represent transport capacities, but they can also be simply used to limit the growth of individual matrix elements with respect to the prior matrix.
In the next section we briefly introduce at the standard biproportional matrix balancing model and its optimization formulation as a maximum entropy model. In section 3 the extended model is formulated and analyzed. In section 4, finally, an efficient solution algorithm is formulated, which is based on the coordinate descent method applied to the dual problem.
The problem of the standard two-dimensional matrix balancing essentially
consist in finding appropriate factors ![]() and
and ![]() for each
origin
for each
origin ![]() and destination
and destination ![]() so that when multiplied
to the corresponding rows and columns of the prior matrix
so that when multiplied
to the corresponding rows and columns of the prior matrix ![]() the marginal totals of resulting matrix
the marginal totals of resulting matrix ![]() correspond to the
given productions
correspond to the
given productions ![]() and attractions
and attractions ![]() . This can be expressed
with the following set of equations:
. This can be expressed
with the following set of equations:
It is easy to show that the above problem can also be expressed as the following convex optimization problem (also referred to as maximum entropy transportation problem):
Defining ![]() and
and ![]() as the dual variable associated with constraints
(10) and (11), we obtain from the Kuhn-Tucker
optimality conditions the following functional form
as the dual variable associated with constraints
(10) and (11), we obtain from the Kuhn-Tucker
optimality conditions the following functional form
![]()
which correspond exactly to (1) when using the following substitutions
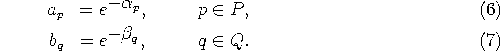
The dual formulation of problem (4) can be written as the following unconstrained optimization problem:
![]()
The standard biproportional matrix balancing model is know to be
always feasible when ![]() and
and ![]() for
all
for
all ![]() .
.
Problems which have ![]() for some O-D pairs can also be handled
in this framework. But in this case, the O-D pairs with
for some O-D pairs can also be handled
in this framework. But in this case, the O-D pairs with ![]() are not to be considered part of the set PQ and
are not to be considered part of the set PQ and ![]() is used
for these O-D pairs where necessary, e.g. where it appears in a sum
over origins or destinations.
is used
for these O-D pairs where necessary, e.g. where it appears in a sum
over origins or destinations.
Note, however, that problems with ![]() for some O-D pairs
are not always feasible. In this case, there is no easy method
to determine the feasibility of a problem a priori, so that the primal
feasibility of a solution found by a dual algorithm always has
to be checked explicitly.
for some O-D pairs
are not always feasible. In this case, there is no easy method
to determine the feasibility of a problem a priori, so that the primal
feasibility of a solution found by a dual algorithm always has
to be checked explicitly.
We now turn our attention to an extension of the model defined in the
previous section in which explicit upper bounds ![]() are imposed on the
resulting matrix elements
are imposed on the
resulting matrix elements ![]() . Since imposing upper bounds will
have a direct impact on the functional form of the resulting model,
it is not possible to formulate the extended model by simply
adding a further constraint to problem (1)-(11).
. Since imposing upper bounds will
have a direct impact on the functional form of the resulting model,
it is not possible to formulate the extended model by simply
adding a further constraint to problem (1)-(11).
However, the minimization problem (4) lends itself very well for an extension by adding upper bound constraints. This leads to the following extended problem formulation:
subject to
Using again ![]() and
and ![]() as the dual variables associated with the
production (=refprod) and attraction constraints (=refattr) and the
new dual variables
as the dual variables associated with the
production (=refprod) and attraction constraints (=refattr) and the
new dual variables ![]() for the upper bound constraints (12),
we can state the Kuhn-Tucker optimality conditions for the above problem
as follows:
for the upper bound constraints (12),
we can state the Kuhn-Tucker optimality conditions for the above problem
as follows:
The optimality condition (13) can be rewritten to yield the following functional form for the resulting model:
By applying the complementary slackness conditions (14) for the
dual variable ![]() and distinguishing between the cases
and distinguishing between the cases ![]() and
and
![]() , (15) becomes
, (15) becomes
![]()
which can be written even more concisely as
Note that the above model formulation does no longer explicitly contain the
dual variables ![]() .
.
Without loss of generality we can assume that ![]() for all
for all ![]() ,
as matrix elements
,
as matrix elements ![]() can always be forced to zero by setting
can always be forced to zero by setting ![]() (and removing the corresponding O-D pairs from the set PQ, as explained in
section 2).
(and removing the corresponding O-D pairs from the set PQ, as explained in
section 2).
The next step is to formulate the Lagrangian dual for problem (9) which becomes
Note that, except for the non-negativity of ![]() ,
the dual problem is essentially unconstrained. For this type of problem
the a simple method of successive coordinate descent is know to converge
to the optimal solution (see e.g. Luenberger 1984). Thus, it can be used
to solve the dual problem (18) and find the optimal values of the dual
variables. If the primal problem (9) is feasible, the
optimal values of the dual variables
,
the dual problem is essentially unconstrained. For this type of problem
the a simple method of successive coordinate descent is know to converge
to the optimal solution (see e.g. Luenberger 1984). Thus, it can be used
to solve the dual problem (18) and find the optimal values of the dual
variables. If the primal problem (9) is feasible, the
optimal values of the dual variables ![]() and
and ![]() can be inserted
into (17) to find the optimal solution of the primal problem.
can be inserted
into (17) to find the optimal solution of the primal problem.
Applying the coordinate descent method to the dual problem (18)
means solving cyclically the first order optimality conditions for the
corresponding dual variables. This implies finding the zeros for the
partial derivatives of the dual objective function with respect to
all ![]() and
and ![]() , and all non-zero
, and all non-zero ![]() :
:
By observing that (21) is equivalent to (17), it is easy to see that conditions (19) and (21) can be combined into the simpler production conditions
and the conditions (20) and (21) combine into the simpler attraction conditions
Solving (22) for ![]() will simultaneously satisfy the
first order conditions (19) for origin p and
(21) for all
will simultaneously satisfy the
first order conditions (19) for origin p and
(21) for all ![]() related to origin p.
In the same manner solving (23) for
related to origin p.
In the same manner solving (23) for ![]() will simultaneously
satisfy the first order conditions (20) for destination q
and (21) for all
will simultaneously
satisfy the first order conditions (20) for destination q
and (21) for all ![]() related to destination
q.
related to destination
q.
Before turning our attention to the solution algorithm, let us briefly
look at the question of feasibility.
The introduction of upper bounds influences the feasibility in a similarly
complex manner as do the zeroes in the matrix ![]() . While of course
the conditions
. While of course
the conditions
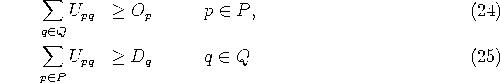
are necessary conditions for feasibility, they are by no means sufficient.
The proposed solution algorithm can be classified as a coordinate descent method applied to the dual problem formulation. As it is based on iteratively solving equations (22) and (23), it actually does not optimize along dual coordinates one by one, but always satisfies the first order conditions simultaneously for all dual variables associated with either one origin or one destination, (which should result in an improved convergence compared to a one-by-one coordinate descent method).
Algorithm 1 describes the basic algorithm proposed to solve the
biproportional matrix balancing problem with upper bounds (9).
This algorithm assumes that equations of the type
![]() can be solved for x.
How this can be done efficiently is shown further on in Algorithm 2.
can be solved for x.
How this can be done efficiently is shown further on in Algorithm 2.
Algorithm 1:
- 0. Initialization
Setfor
and set k:=1.
- 1. Balance origins
For each originsolve the equation
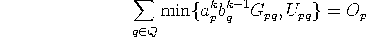
for variable
by applying Algorithm 2.
- 2. Balance destinations
For each destinationsolve the equation
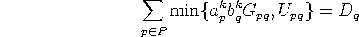
for variable
by applying Algorithm 2.
- 3. Test stopping criteria
If convergence is reached for the the multipliersand
,
e.g., then go to step 4,
otherwise set k:=k+1 and return to step 1.
- 4. Compute primal solution
If the maximum production constraint violation for allis smaller than some predefined tolerance value, i.e.
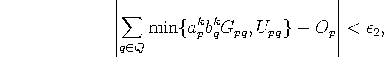
then compute the optimal primal solution

otherwise the primal problem is infeasible. STOP.
Now let us consider the subproblem how to find the factor x which solves an equation of the form
This type of problem occurs in step 1 of Algorithm 1 with
i=q, ![]() ,
, ![]() , and in step 3
with i=q,
, and in step 3
with i=q, ![]() ,
, ![]() .
Without loss of generality we can assume that
.
Without loss of generality we can assume that ![]() and
and ![]() for
all
for
all ![]() . If there were any elements i with
. If there were any elements i with ![]() and/or
and/or ![]() ,
these can simply be dropped, since they do not influence the solution of
(26) at all.
,
these can simply be dropped, since they do not influence the solution of
(26) at all.
This type of problem can be solved by first sorting the elements i according
to their ![]() ratios and then scanning the elements linearly in this order
and checking if the optimal value x lies in the range between of
two consecutive
ratios and then scanning the elements linearly in this order
and checking if the optimal value x lies in the range between of
two consecutive ![]() ratios. This leads to the formulation of the
following algorithm:
ratios. This leads to the formulation of the
following algorithm:
Algorithm 2: (Solve)
- 0. Initialization
Setand U=T
- 1. Sort elements
Sort the elements i in increasing order ofratios.
- 2. Scan elements
Using the order established in step 1, do for each i:
Ifthen
setand
,
else
go to step 3.
If this point is reached after having scanned all elements, then the problem is infeasible, STOP.- 3. Compute optimal solution
Set the solution to x=U/F and STOP.
So far, the above algorithms have only been implemented in a ``quick and dirty'' manner purely for testing purposes. In the few examples tested so far (all based on data taken from the standard EMME/2 Winnipeg data bank using 154 traffic zones), the algorithm has been found to converge quite rapidly (4-7 iterations) to the optimal solution. But of course, further tests are needed.
The methodology of introducing upper bounds is presented in this note only for the biproportional matrix balancing. However, it can most likely be applied directly to other related problems, such as the multi-proportional matrix balancing or Evans and Kirby's three-dimensional matrix balancing.